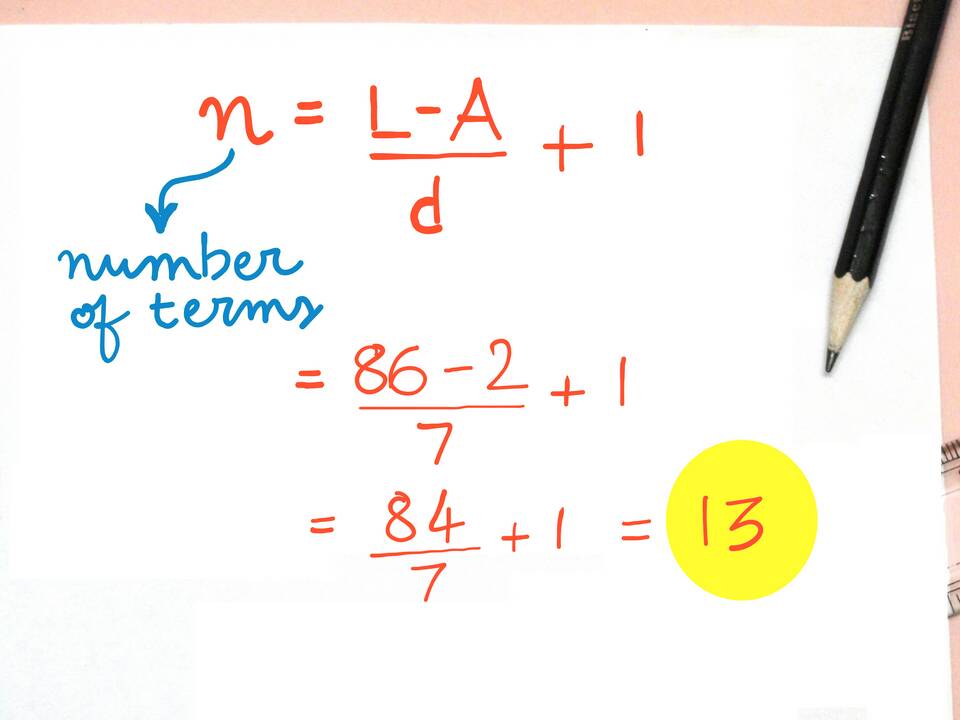Вычисление суммы первых членов прогрессии - важная задача в математике, имеющая практическое применение в экономике и естественных науках. Рассмотрим методы расчета для арифметической и геометрической прогрессий.
Содержание
Вычисление суммы первых членов прогрессии - важная задача в математике, имеющая практическое применение в экономике и естественных науках. Рассмотрим методы расчета для арифметической и геометрической прогрессий.
Арифметическая прогрессия
| Параметр | Обозначение |
| Первый член | a₁ |
| Разность прогрессии | d |
| Количество членов | n |
Формула суммы
Sₙ = n/2 × (2a₁ + d(n-1))
Или альтернативно: Sₙ = n/2 × (a₁ + aₙ)
Геометрическая прогрессия
| Параметр | Обозначение |
| Первый член | b₁ |
| Знаменатель прогрессии | q |
| Количество членов | n |
Формула суммы
Sₙ = b₁ × (qⁿ - 1)/(q - 1) (при q ≠ 1)
Для q = 1: Sₙ = n × b₁
Примеры расчетов
| Тип прогрессии | Данные | Расчет | Результат |
| Арифметическая | a₁=5, d=3, n=4 | 4/2 × (2×5 + 3×3) = 2 × (10 + 9) = 38 | 38 |
| Геометрическая | b₁=2, q=3, n=3 | 2 × (3³-1)/(3-1) = 2 × 26/2 = 26 | 26 |
Практическое применение
- Финансовые расчеты (кредиты, вклады)
- Физика (равноускоренное движение)
- Биология (рост популяций)
- Компьютерные науки (алгоритмы)
Особые случаи
- Бесконечно убывающая геометрическая прогрессия (|q| < 1)
- Прогрессии с переменными параметрами
- Комбинированные прогрессии
Проверка правильности расчета
| Метод проверки | Описание |
| Последовательное сложение | Суммирование всех членов по отдельности |
| Математическая индукция | Доказательство для общего случая |
Понимание методов вычисления суммы первых членов прогрессии позволяет решать широкий круг математических и прикладных задач. Для сложных случаев рекомендуется использовать специализированное программное обеспечение.
