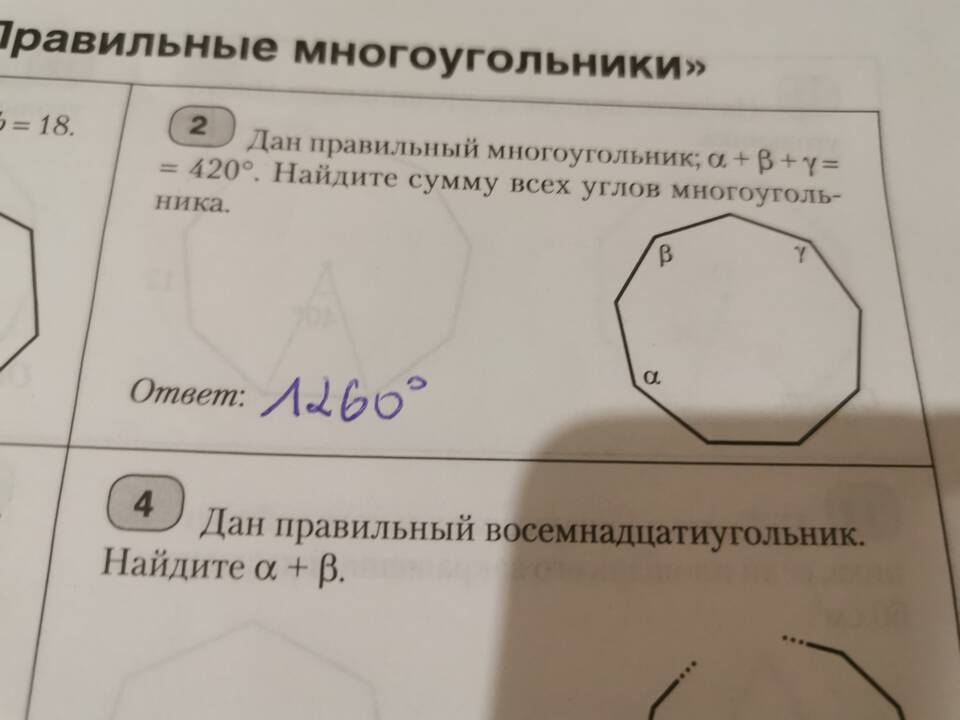
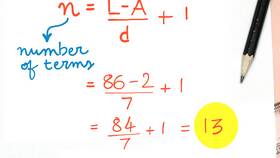Сумма внутренних углов выпуклого многоугольника вычисляется по формуле: S = (n - 2) × 180°, где n - количество сторон многоугольника.
Содержание
Основная формула расчета
Сумма внутренних углов выпуклого многоугольника вычисляется по формуле: S = (n - 2) × 180°, где n - количество сторон многоугольника.
Пошаговый алгоритм расчета
1. Определение количества сторон
- Посчитайте количество сторон (вершин) многоугольника
- Убедитесь, что многоугольник выпуклый (все углы меньше 180°)
- Запишите количество сторон как переменную n
2. Применение формулы
| Тип многоугольника | Пример расчета |
| Треугольник (3 стороны) | (3-2)×180° = 180° |
| Четырехугольник (4 стороны) | (4-2)×180° = 360° |
| Пятиугольник (5 сторон) | (5-2)×180° = 540° |
Частные случаи
Правильные многоугольники
- Все стороны и углы равны
- Каждый угол = (n-2)×180° / n
- Пример: правильный шестиугольник - каждый угол 120°
Звездчатые многоугольники
Для невыпуклых (звездчатых) многоугольников формула остается прежней, но требует осторожности в определении количества сторон.
Практические примеры
Пример 1: Семиугольник
- Количество сторон n = 7
- Применяем формулу: (7-2)×180° = 5×180° = 900°
- Сумма углов равна 900°
Пример 2: Десятиугольник
| Шаг | Расчет |
| 1. Определение n | n = 10 |
| 2. Подстановка в формулу | (10-2)×180° |
| 3. Вычисление | 8×180° = 1440° |
Доказательство формулы
Метод разбиения на треугольники
- Из одной вершины проведите диагонали во все другие вершины
- Многоугольник разобьется на (n-2) треугольника
- Сумма углов каждого треугольника 180°
- Общая сумма: (n-2) треугольников × 180°
Важные замечания
- Формула работает только для простых многоугольников без самопересечений
- Для многоугольников с дырами применяются другие методы
- Внешние углы многоугольника всегда суммируются до 360°
